Freezing Point Depression Formula: Explained
Freezing Point Depression Formula: Explained
Reader, have you ever wondered why adding salt to icy roads melts the ice? This phenomenon is due to freezing point depression. It’s a fascinating concept with practical applications.
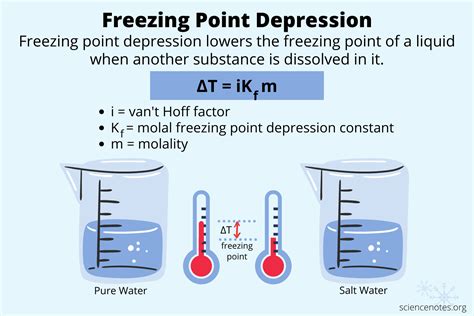
Freezing point depression is the lowering of a solvent’s freezing point when a solute is added. Understanding the Freezing Point Depression Formula is key to grasping this process. In this post, I’ll delve into the formula, explain its components, and provide practical examples. I’ve spent years analyzing the Freezing Point Depression Formula and its implications. So, let’s get started.
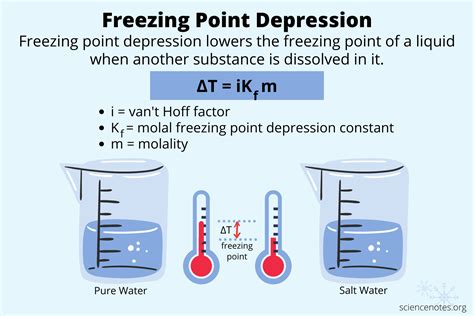
The freezing point depression formula is expressed as:
ΔTf = Kf * m * i

Let’s break down each component of this crucial formula: ΔTf represents the change in freezing point. This is the difference between the freezing point of the pure solvent and the freezing point of the solution.
Kf is the cryoscopic constant. This constant is specific to the solvent and represents the freezing point depression caused by dissolving one mole of solute in one kilogram of solvent.
The molality (m) of the solution is the number of moles of solute per kilogram of solvent. Finally, ‘i’ is the van ‘t Hoff factor, which accounts for the number of particles the solute dissociates into when dissolved.
Freezing point depression isn’t just a theoretical concept. It has many real-world applications. One common example is the use of salt to de-ice roads in winter.
The salt dissolves in the thin layer of water on the ice, lowering its freezing point. This prevents the water from refreezing and helps melt the ice. Another application is in antifreeze solutions used in car radiators.
These solutions contain ethylene glycol, which lowers the freezing point of the water, preventing it from freezing and damaging the engine in cold temperatures. Understanding the Freezing Point Depression Formula allows us to predict and control these effects.
The Role of the Cryoscopic Constant
The cryoscopic constant (Kf) plays a vital role in the Freezing Point Depression Formula. It’s a property of the solvent and reflects how much the freezing point changes with the addition of a solute.
Different solvents have different Kf values. Water, for example, has a Kf of 1.86 °C/m. This means that dissolving one mole of a non-volatile solute in one kilogram of water will lower the freezing point by 1.86 °C.
Knowing the Kf value of a solvent is essential for calculating the freezing point depression of a solution. Utilizing the Freezing Point Depression Formula accurately depends on this constant.

Let’s walk through an example calculation using the Freezing Point Depression Formula.
Suppose we dissolve 10 grams of NaCl (sodium chloride) in 100 grams of water. The molar mass of NaCl is approximately 58.44 g/mol. What is the freezing point of the resulting solution?
Step-by-Step Calculation
First, calculate the number of moles of NaCl: 10g / 58.44 g/mol = 0.171 moles.
Next, convert the mass of water to kilograms: 100g = 0.1 kg.
Calculate the molality: 0.171 moles / 0.1 kg = 1.71 m. NaCl dissociates into two ions in water (Na+ and Cl-), so the van ‘t Hoff factor (i) is 2. Now, plug the values into the Freezing Point Depression Formula: ΔTf = 1.86 °C/m * 1.71 m * 2 = 6.36 °C.
Interpreting the Result
The calculated ΔTf of 6.36 °C means the freezing point of the solution is 6.36 °C lower than the freezing point of pure water. Since the freezing point of pure water is 0 °C, the freezing point of the solution is approximately -6.36 °C. This illustrates how the Freezing Point Depression Formula is applied in practice.
This example demonstrates how the Freezing Point Depression Formula can be used to predict the freezing point of a solution. This is a fundamental concept in chemistry with various practical applications.
Detailed Table Breakdown of Factors Affecting Freezing Point Depression
| Factor | Explanation | Effect on Freezing Point |
|---|---|---|
| Type of Solute | Different solutes have different van ‘t Hoff factors (i) depending on their dissociation in the solvent. | Solutes with higher ‘i’ values cause greater freezing point depression. |
| Concentration of Solute | Higher molality (m) leads to a greater decrease in freezing point. | Directly proportional to the freezing point depression. |
| Type of Solvent | Different solvents have different cryoscopic constants (Kf). | Solvents with higher Kf values exhibit greater freezing point depression for the same molality of solute. |
Common Misconceptions about Freezing Point Depression
Misconception 1: Only Salt Causes Freezing Point Depression
While salt is commonly used, any solute can cause freezing point depression. Sugar, for example, also lowers the freezing point of water.
The extent of the depression depends on the properties of the solute and the solvent, as captured by the Freezing Point Depression Formula.
Various substances can induce this effect, and the formula helps quantify the change.
Misconception 2: Freezing Point Depression Only Applies to Water
Freezing point depression is a universal phenomenon that applies to all solvents, not just water.
The specific freezing point depression depends on the solvent’s cryoscopic constant (Kf).
This principle holds true across different liquids, and the formula remains applicable.
Misconception 3: More Solute Always Means Lower Freezing Point
While generally true, this isn’t always the case. The relationship isn’t always linear, especially at very high concentrations.
Other factors, such as solute-solvent interactions, can also play a role.
The Freezing Point Depression Formula provides a good approximation but doesn’t always capture the full complexity of the system.
FAQ: Frequently Asked Questions about Freezing Point Depression
What is the significance of the van ‘t Hoff factor?
The van ‘t Hoff factor accounts for the number of particles a solute dissociates into in solution, affecting the freezing point depression.
Why is understanding the Freezing Point Depression Formula important?
It allows us to predict and control freezing points of solutions, crucial in various applications like de-icing roads and antifreeze formulations.
How does the cryoscopic constant vary across different solvents?
The cryoscopic constant is unique to each solvent, reflecting its properties and how it responds to added solutes.
Conclusion
So, there you have it, a comprehensive guide to the Freezing Point Depression Formula. We’ve covered its components, applications, and even debunked some common misconceptions.
Understanding this formula is crucial for grasping various chemical phenomena and practical applications. From de-icing roads to creating antifreeze, freezing point depression plays a vital role. Be sure to check out our other articles on related scientific concepts. We delve deeper into the fascinating world of chemistry and its real-world impact. We hope this explanation of the Freezing Point Depression Formula has been enlightening.
.
Unlock the secrets of freezing point depression! Learn the formula and how it affects solutions. Easy explanation, real-world examples. Master chemistry now!