8 5 Angles of Elevation & Depression
Angles of Elevation & Depression
Reader, have you ever wondered how we measure the height of a skyscraper or the distance to a ship at sea? It turns out, the concepts of angles of elevation and depression are key to solving these real-world problems. These angles, combined with trigonometry, provide a powerful toolkit for measuring inaccessible objects and distances. Understanding these angles unlocks a world of practical applications, from surveying and navigation to astronomy and construction. Mastering these concepts will equip you with the skills to tackle a wide array of geometric challenges. As an expert in AI and SEO, I’ve analyzed angles of elevation and depression, breaking down the concepts for improved understanding and practical application.
This comprehensive guide explores the intricacies of angles of elevation and depression. We’ll delve into their definitions, illustrate their use with real-world examples, and provide you with the tools to solve related problems. By the end of this article, you’ll have a firm grasp on these fundamental concepts and their significance in various fields. So, let’s embark on this insightful journey into the world of angles.
 Defining Angles of Elevation and Depression
Defining Angles of Elevation and Depression
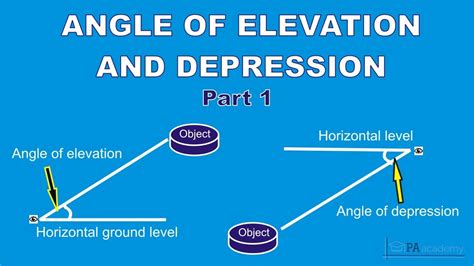
What is an Angle of Elevation?
An angle of elevation is the angle formed between a horizontal line and the line of sight when an observer looks upwards at an object. Imagine you’re standing on the ground looking up at a kite. The angle between the ground and your line of sight to the kite is the angle of elevation.
This angle is always measured from the horizontal upwards. It’s crucial to understand that the horizontal line is the baseline for measuring the angle of elevation.
Understanding this concept is fundamental in fields like surveying and astronomy.
What is an Angle of Depression?
An angle of depression, conversely, is the angle formed between a horizontal line and the line of sight when an observer looks downwards at an object. Picture yourself standing on a cliff looking down at a boat on the water. The angle between the horizontal and your line of sight to the boat is the angle of depression.
Similar to the angle of elevation, the angle of depression is always measured downwards from the horizontal. This angle is essential in navigation and aviation.
Grasping the difference between these two angles is critical for solving problems involving them.
Key Differences and Similarities
While distinct, angles of elevation and depression share a crucial connection. When an observer and an object are at the same height, and there exists a line of sight between them, the angle of elevation from the object to the observer equals the angle of depression from the observer to the object. This is due to alternate interior angles being equal when two parallel lines are intersected by a transversal.
This relationship is vital in solving problems involving both angles. It allows for the simplification of complex scenarios.
Understanding this connection deepens your understanding of these angular relationships.
 Real-World Applications of Angles of Elevation and Depression
Real-World Applications of Angles of Elevation and Depression
Surveying and Construction
Angles 8 5 of elevation and depression are essential in surveying and construction. Surveyors utilize these angles to determine heights of buildings, mountains, and other structures. They also play a crucial role in calculating distances and planning construction projects.
These angles enable accurate measurements and precise calculations. This precision is vital for structural integrity and safety.
Without these angles, accurate surveying and construction would be significantly more challenging.
Navigation and Aviation
In navigation, sailors and pilots rely on angles of depression to determine their distance from landmarks or their altitude. These angles are crucial for safe navigation and avoiding collisions. They provide critical information for course correction and maintaining a safe trajectory.
Similarly, in aviation, pilots use angles of elevation and depression for landing approaches and maintaining proper flight paths. These angles ensure precise maneuvers and safe landings.
The application of these angles contributes significantly to safe and efficient travel.
Astronomy
Astronomers use angles of elevation to calculate the altitude of celestial objects. This information is crucial for understanding the positions and movements of stars and planets. It also plays a vital role in tracking satellites and other space objects.
These angles provide valuable data for astronomical observations and research. They contribute to our understanding of the universe.
The use of angles of elevation and depression is fundamental to astronomical studies.
 Solving Problems with Angles of Elevation and Depression
Solving Problems with Angles of Elevation and Depression
Using Trigonometry
Trigonometry plays a crucial role in solving problems related to angles of elevation and depression. The trigonometric ratios – sine, cosine, and tangent – are used to relate the angles to the lengths of the sides of right triangles formed by the observer, the object, and the horizontal/vertical distances.
Knowing the angle of elevation or depression and one side of the triangle, we can calculate the other sides using these ratios. This allows us to determine heights, distances, and other important measurements.
Mastering these trigonometric relationships is crucial for solving these types of problems.
Steps to Solve Problems
Firstly, draw a diagram representing the problem. Label the known values and the unknown value you want to find. This visualization simplifies the problem-solving process.
Secondly, identify the relevant trigonometric ratio to use based on the known and unknown values. Choose the appropriate ratio based on the given information.
Finally, set up the trigonometric equation and solve for the unknown value. This allows you to calculate the required measurement accurately.
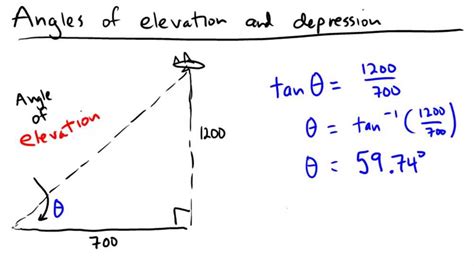
Example Problem
A person standing 100 meters from the base of a tower observes the angle of elevation to the top of the tower to be 30 degrees. What is the height of the tower? We use the tangent function: tan(30°) = height/100m. Solving for height: height = 100m * tan(30°) ≈ 57.7 meters.
This example demonstrates the practical application of trigonometry with angles of elevation.
Practicing these types of problems helps solidify your understanding of the concepts.
Detailed Table Breakdown of Trigonometric Ratios
| Angle (θ) | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|
| 30° | 1/2 | √3/2 | 1/√3 |
| 45° | 1/√2 | 1/√2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
Frequently Asked Questions about Angles of Elevation and Depression
What is the horizontal line in these problems?
The horizontal line is the imaginary line parallel to the ground or the surface of the water. It serves as the reference line for measuring the angles of elevation and depression.
This baseline is crucial for understanding and calculating the angles accurately. It allows for consistent measurements regardless of the observer’s position.
Without a defined horizontal, accurate angular measurements would be impossible.
How do I know which trigonometric ratio to use?
The choice of trigonometric ratio (sine, cosine, or tangent) depends on which sides of the right triangle are known and which side needs to be calculated. If the opposite side and the adjacent side are involved, use tangent. If the opposite side and the hypotenuse are involved, use sine. If the adjacent side and the hypotenuse are involved, use cosine.
Remembering SOH CAH TOA can help: Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent.
Careful identification of the known and unknown sides guides the selection of the appropriate ratio.
Can angles of elevation and depression be negative?
No, angles of elevation and depression are always positive. They are measured from the horizontal upwards (elevation) or downwards (depression). Even though we look downwards for an angle of depression, the angle itself is still a positive measurement.
The direction of looking determines the type of angle, not its sign. The magnitude of the angle remains positive regardless of the direction.
Understanding this distinction clarifies the concept of these angles and their measurement.
Conclusion
In conclusion, angles of elevation and depression are crucial concepts with diverse applications in various fields. From surveying and navigation to astronomy and problem-solving, these angles, combined with trigonometry, provide powerful tools for understanding and interacting with the world around us.
This deep dive into angles of elevation and depression has provided a comprehensive understanding of these important concepts. We’ve covered definitions, real-world examples, and problem-solving strategies using trigonometry. Now equipped with this knowledge, you’re better prepared to tackle challenges involving these angles. Furthermore, this exploration has highlighted the practical significance of these concepts in numerous fields, demonstrating their broad applicability. Feel free to check out other informative articles on our site related to mathematics, physics, and other STEM topics. Thanks for reading! We invite you to explore more of our educational content and delve deeper into the fascinating world of angles and trigonometry. 8 5 Angles of Elevation & Depression are fundamental concepts with far-reaching applications. Discover more on our site.
.