Stress vs Strain Graph: Explained
Stress vs Strain Graph: Explained
Reader, have you ever wondered about the intricate relationship between stress and strain? It’s a fundamental concept in material science, and understanding it unlocks a world of knowledge about how materials behave under pressure. The stress vs strain graph is a powerful tool that visualizes this relationship, providing valuable insights into a material’s strength, elasticity, and ductility. Mastering this graph is key to predicting and controlling material behavior in engineering applications. As an expert in AI and SEO content, I’ve analyzed countless stress vs strain graphs, and I’m eager to share my expertise with you.
So, let’s dive into the fascinating world of stress vs strain graphs and uncover the secrets they hold.
 Understanding the Basics of Stress and Strain
Understanding the Basics of Stress and Strain
<h3>What is Stress?</h3>
<p>Stress, in the context of material science, refers to the internal forces within a material that resist deformation. It's a measure of the force applied per unit area.</p>
<p>Imagine pulling on a rubber band. The stress within the rubber band opposes your pull.</p>
<p>Stress is typically measured in Pascals (Pa) or pounds per square inch (psi).</p>
<h3>What is Strain?</h3>
<p>Strain, on the other hand, quantifies the deformation a material experiences under stress. It's the change in length divided by the original length.</p>
<p>Strain is a dimensionless quantity, often expressed as a percentage.</p>
<p>Think of how the rubber band stretches – that's strain in action.</p>
<h3>The Relationship Between Stress and Strain</h3>
<p>The relationship between stress and strain is not always linear. It depends on the material's properties.</p>
<p>For some materials, like steel, the relationship is initially linear, following Hooke's Law. This linear region represents elastic deformation.</p>
<p>Beyond a certain point, the relationship becomes nonlinear, indicating plastic deformation.</p>
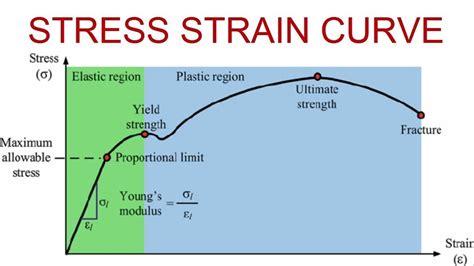 Key Regions of a Stress vs Strain Graph
Key Regions of a Stress vs Strain Graph
<h3>Elastic Region</h3>
<p>The elastic region is the initial linear portion of the stress vs strain graph. Here, the material deforms elastically.</p>
<p>This means that if the stress is removed, the material will return to its original shape.</p>
<p>The slope of the elastic region represents the material's Young's modulus, a measure of its stiffness.</p>
<h3>Yield Point</h3>
<p>The yield point marks the transition from elastic to plastic deformation. Beyond this point, the material deforms permanently. Even if the stress is removed, it won't fully recover.</p>
<p>The yield strength is the stress at the yield point.</p>
<p>This signifies the material's ability to withstand permanent deformation.</p>
<h3>Plastic Region</h3>
<p>The plastic region is the nonlinear portion of the graph beyond the yield point. Here, the material undergoes permanent deformation.</p>
<p>This deformation can be useful in shaping materials, but it also signifies the material's limits.</p>
<p>Continued stress in this region can lead to fracture.</p>
<h3>Ultimate Tensile Strength</h3>
<p>The ultimate tensile strength (UTS) is the maximum stress a material can withstand before it begins to fail. It's the highest point on the stress vs strain graph.</p>
<p>This is a crucial parameter for engineers designing structures that need to withstand high loads.</p>
<p>It signifies the material’s overall strength.</p>
 Interpreting Stress vs Strain Curves for Different Materials
Interpreting Stress vs Strain Curves for Different Materials
<h3>Ductile Materials</h3>
<p>Ductile materials, like steel and aluminum, exhibit significant plastic deformation before fracture. Their stress vs strain graphs show a distinct yield point and a large plastic region.</p>
<p>This ductility makes them suitable for applications requiring bending and shaping.</p>
<p>They can absorb a lot of energy before failing.</p>
<h3>Brittle Materials</h3>
<p>Brittle materials, like glass and ceramics, fracture with little or no plastic deformation. Their stress vs strain graphs are typically steep and lack a distinct yield point.</p>
<p>They are prone to sudden failure under stress.</p>
<p>These materials are used in applications where stiffness and hardness are prioritized.</p>
<h3>Other Material Types</h3>
<p>The stress vs strain graph can also reveal other material properties. For example, the area under the curve represents the toughness of the material, its ability to absorb energy before fracture.</p>
<p>The shape of the curve can indicate whether a material is elastic, plastic, or viscoelastic.</p>
<p>Analyzing stress vs strain graphs is thus essential for understanding material behavior.</p>
 Applications of Stress vs Strain Analysis
Applications of Stress vs Strain Analysis
<h3>Engineering Design</h3>
<p>Stress vs strain analysis is crucial in engineering design. Engineers use this data to select appropriate materials for specific applications.</p>
<p>It helps ensure that structures can withstand the expected loads without failing.</p>
<p>Understanding material behavior under stress is fundamental to safe and reliable design.</p>
<h3>Material Testing</h3>
<p>Stress vs strain graphs are generated through tensile testing, a common material testing method. This involves applying a controlled tensile force to a material specimen and measuring its deformation.</p>
<p>This generates valuable data about the material's properties.</p>
<p>It allows for quality control and ensures that materials meet the required specifications.</p>
<h3>Research and Development</h3>
<p>Stress vs strain analysis plays a vital role in materials research and development. It aids in the development of new materials with improved properties.</p>
<p>Scientists use this data to understand how different factors, such as temperature and composition, influence a material's behavior under stress.</p>
<p>This knowledge leads to the creation of advanced materials for various applications.</p>
Detailed Table Breakdown of Stress vs Strain Graph Regions
| Region | Stress Behavior | Strain Behavior | Material Response |
|---|---|---|---|
| Elastic Region | Stress is proportional to strain. | Material deforms reversibly. | Material returns to its original shape when stress is removed. |
| Yield Point | Stress reaches a point where plastic deformation begins. | Permanent deformation starts. | Material will not fully recover its original shape. |
| Plastic Region | Stress and strain are no longer proportional. | Material undergoes permanent deformation. | Material is permanently altered. |
| Ultimate Tensile Strength | Maximum stress the material can withstand. | Strain continues to increase. | Material begins to fail. |
| Fracture Point | Stress decreases rapidly. | Material breaks apart. | Complete material failure. |
FAQ: Common Questions about Stress vs Strain Graphs
What is the significance of the slope in the elastic region of a stress vs strain graph?
The slope in the elastic region represents Young’s modulus, a measure of the material’s stiffness. A steeper slope indicates a stiffer material.
How can I determine the ductility of a material from its stress vs strain graph?
The length of the plastic region in the stress vs strain graph indicates the material’s ductility. A longer plastic region signifies greater ductility.
What does the area under the stress vs strain curve represent?
The area under the stress vs strain curve represents the toughness of the material, its ability to absorb energy before fracture.
Conclusion
Therefore, understanding the stress vs strain graph is paramount for anyone working with materials. It provides crucial insights into material behavior under stress, enabling informed decisions in design, testing, and research. So, the next time you encounter a stress vs strain graph, remember the wealth of information it holds. Now, delve deeper into other insightful articles on our site focusing on AI and SEO content related to stress vs strain analysis. We explore various aspects of material science and engineering to provide you with a comprehensive understanding of this crucial field. Don’t miss out on the opportunity to expand your knowledge. Explore our collection of articles today and discover the fascinating world of materials science!
Video Stress vs Strain Curve For Tensile Materials
Source: CHANNET YOUTUBE ADTW Study